多水平验证性因子分析是一种在Mplus中用于分析复杂调查数据的方法。这种方法包括两个或更多水平的数据,每个水平代表一个不同的数据来源或测量层次。例如, 你的数据来自于多个学校的学生,学生是以学校为单位抽取得到的, 那么学生数据之间存在相关性。 比较适合多水平的验证性因子分析(Multilevel Confirmatory Factor Analysis,以下简称 MCFA 。
在纵向数据中, 一个个体会被测量多次, 我们将每个时间点的数据作为样本, 那么时间点是嵌套在个体之中的,
这种结构的数据与前面的嵌套数据结构是一致的。
嵌套数据中, 我们有时候用到了潜变量进行建模, 比如做多水平的结构方程模型, 这时候需要提前做验证性因子分析。
所以本篇教程是后续多水平结构方程模型教程的预备课程。
什么是纵向数据
Longitudinal Data指的是在同一组个体或人群中,随着时间的推移追踪观察,记录同一组数据的情况。例如,一个研究小组跟踪一组年轻人的成长过程,记录他们的身高、体重、饮食、运动等数据随时间的变化。这种数据类型在心理学、医学、社会学等领域的研究中非常常见。
这种数据有很多存储的格式, 一种常见的格式被称为“长格式”, 例如:
| 受试者ID | 测量轮次 | 测量值 |
|---|---|---|
| 001 | 1 | 25.5 |
| 001 | 2 | 26.2 |
| 001 | 3 | 25.8 |
| 001 | 4 | 26.1 |
| 002 | 1 | 24.9 |
| 002 | 2 | 25.3 |
| 002 | 3 | 25.1 |
| 002 | 4 | 25.5 |
| … | … | … |
案例介绍
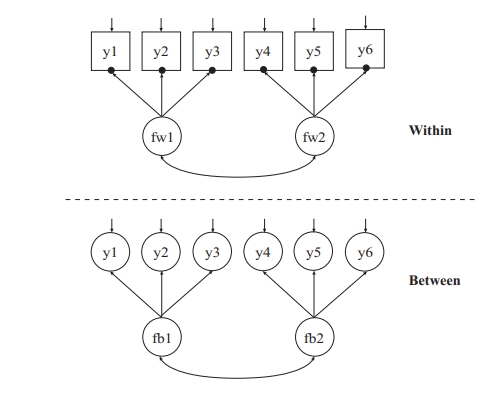
在我们的简单案例中, 我们有两个潜变量, f1 和 f2, 每个潜变量有三个观测指标,
总共6个观测指标, 分别是 y1-y6, 数据当中还有一个变量是ID, 代表每个被试的编码, 我们看下数据:
| y1 | y2 | y3 | y4 | y5 | y6 | ID |
|---|---|---|---|---|---|---|
| 0.081987 | -0.287225 | -2.033206 | -2.032697 | 1.418202 | 0.513686 | 1 |
| -0.928530 | -2.196663 | 3.377093 | 0.525700 | 1.540415 | 0.420246 | 1 |
| -0.884323 | -7.290047 | -0.425843 | -1.776992 | -2.493705 | -0.259916 | 1 |
| 0.901712 | -0.411791 | -2.056783 | 1.971860 | -5.170934 | 0.994531 | 1 |
| -2.199115 | -0.326509 | -2.277330 | -1.955370 | -0.591493 | -1.027715 | 1 |
| 0.000974 | 3.046932 | 0.469873 | -0.927001 | -0.266280 | -3.880203 | 2 |
| -1.448368 | -0.911395 | 1.312358 | 1.142734 | 2.387918 | -3.926418 | 2 |
为什么必须用多水平CFA
普通的CFA要求样本是独立的, 但是我们现在的样本是纵向数据, 比如数据的前5行是一个被试的5个时间点的样本。
这违背了普通CFA的假定, 并且如果你强行做普通的CFA, 你的模型无法解释由于由于样本重复导致的过高的相关性。
普通的验证性因子分析模型如下:
以观测指标y1为例
$$ y1 = h_1 + \lambda_1 f_1 + \epsilon_1 $$
$f_1$是潜变量, 它通过等号右边的算式来预测观测指标y1, 对于所有的被试,在所有时间的观测样本, $h_1$是常数, 意思是不变的, 在上面的方程中起着截距的作用, 和回归上的截距是类似的,它代表了潜变量f1取0的时候y1的值。 但是因为是嵌套数据, $h_1$ 不变这个假定并不能反映真实情况, 很有可能 $h_1$ 因为被试的不同而不同, 即在潜变量f1取0的时候, 每个被试的观测值y1可能是不同的,并且同一个被试不同观测时间的截距可能是相同的。 所以我们可以假定 $h_1$ 是随个体变化的, 即 $h_{1i}$, i表示被试id。
$h_{1i}$是一个变量, 因此我们的模型是这样的:
$$ y1 = h_{1i} + \lambda_{1} f_1 + \epsilon_1 $$
综上所述, 我们把上图中的模型都用数学表达式写出来就是:
$$ y1 = h_{1i} + \lambda_{1} fw_1 + \epsilon \\ y2 = h_{2i} + \lambda_{2} fw_1 + \epsilon \\ y3 = h_{3i} + \lambda_{3} fw_1 + \epsilon \\ y4 = h_{4i} + \lambda_{4} fw_2 + \epsilon \\ y5 = h_{5i} + \lambda_{5} fw_2 + \epsilon \\ y6 = h_{6i} + \lambda_{6} fw_2 + \epsilon \\ h_{1i} = \gamma_{1} fb_1 + \epsilon \\ h_{2i} = \gamma_{2} fb_1 + \epsilon \\ h_{3i} = \gamma_{3} fb_1 + \epsilon \\ h_{4i} = \gamma_{4} fb_2 + \epsilon \\ h_{5i} = \gamma_{5} fb_2 + \epsilon \\ h_{6i} = \gamma_{6} fb_2 + \epsilon \\ $$
多层验证性因子分析如何用MPLUS实现
我们先看代码, 然后再解读。
1 | TITLE: 两层两因子验证性因子分析案例 |
TITLE
TITLE用于指定标题, 你可以写任意你想要的标题, 它不参与分析, 但是帮助你理解和整理结果
DATA
DATA命令用于指定数据文件, 固定写法就是 $ FILE IS$
代码的运行
我们使用R中的Mplusautomation这个库来自动化mplus, 如果你不会R也不用担心, 因为你可以自行在mplus中运行上面的mplus脚本。 为什么我用的是R呢, 因为 Mplusautomation 可以自动化处理很多繁琐的事情, 比如整理结果。
1 | library(MplusAutomation) |
1 | ex9.11_fit$results$summaries[ c("AICC","ChiSqM_Value", "ChiSqM_DF", "CFI", "TLI","RMSEA_Estimate", "SRMR.Within", "SRMR.Between")] |
| AICC | ChiSqM_Value | ChiSqM_DF | CFI | TLI | RMSEA_Estimate | SRMR.Within | SRMR.Between |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 27956.52 | 13.75 | 16 | 1 | 1.006 | 0 | 0.014 | 0.062 |
区分效度
通常区分效度有很多证明的方法, 其中之一就是构建多个因子模型, 从单因子到多因子模型,
就本案例来说,因为我们有两个因子, 如果2因子模型在所有模型中是拟合度最好的,就可以证明我们的变量之间具有区分效度。
下面我们构建一个单因子的模型:
1 | ex9.11_mobj2 <- mplusObject( |
| AICC | ChiSqM_Value | ChiSqM_DF | CFI | TLI | RMSEA_Estimate | SRMR.Within | SRMR.Between |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 28053.53 | 149.483 | 18 | 0.804 | 0.673 | 0.085 | 0.06 | 0.119 |
将两个模型的拟合度整合到一起:
1 | fit1 = ex9.11_fit$results$summaries[ c("AICC","ChiSqM_Value", "ChiSqM_DF", "CFI", "TLI","RMSEA_Estimate", "SRMR.Within", "SRMR.Between")] |
| AICC | ChiSqM_Value | ChiSqM_DF | CFI | TLI | RMSEA_Estimate | SRMR.Within | SRMR.Between | |
|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 两因子 | 27956.52 | 13.750 | 16 | 1.000 | 1.006 | 0.000 | 0.014 | 0.062 |
| 单因子 | 28053.53 | 149.483 | 18 | 0.804 | 0.673 | 0.085 | 0.060 | 0.119 |
参考文献
https://www.scirp.org/journal/paperinformation?paperid=92317
注意
统计咨询请加QQ 2726725926, 微信 mllncn, 统计咨询是收费的,不限软件, 不论什么模型都可以, 只限制于1个研究内.
本文由jupyter notebook转换而来, 您可以在这里下载notebook
可以在微博上@mlln-cn向我免费题问
请记住我的网址: mlln.cn 或者 jupyter.cn


